

In this investigation, we will take a look at the XC plane and how to determine the roots within this plane.
First, let's start with the following function:
![]()
The goal is to determine the roots of this equation, specifically if we are looking at the xc plane.
To gain a better understanding of the equation in the xc plane, let's graph a specific example.
Let's take the cases where a=1, b=1, c=1 and a=2, b=2, and c=2.
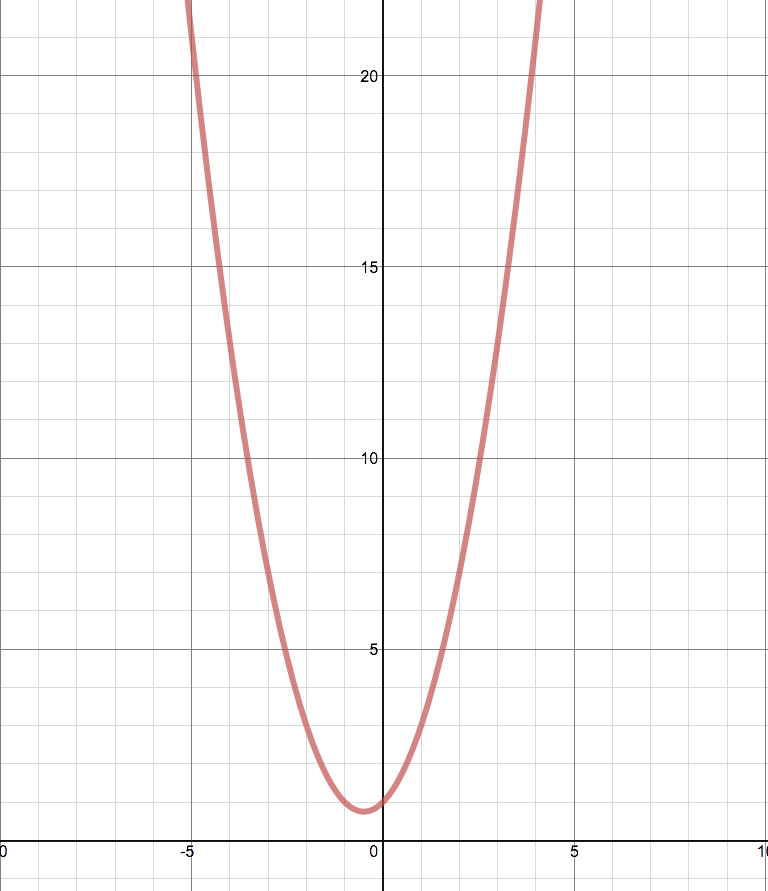 |
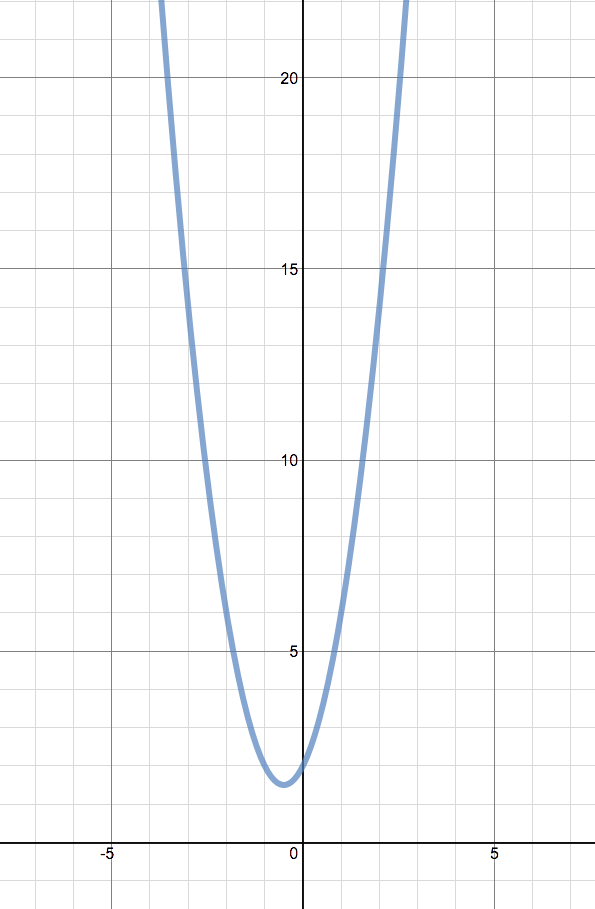 |
|
|
Now, let's take a look at these equations if we are in the xc plane. We can do this by simply replacing the c with a y.
![]()
Now to graph this equation in Desmos or other graphing software, the equation must be rearranged to y=
![]()
![]()
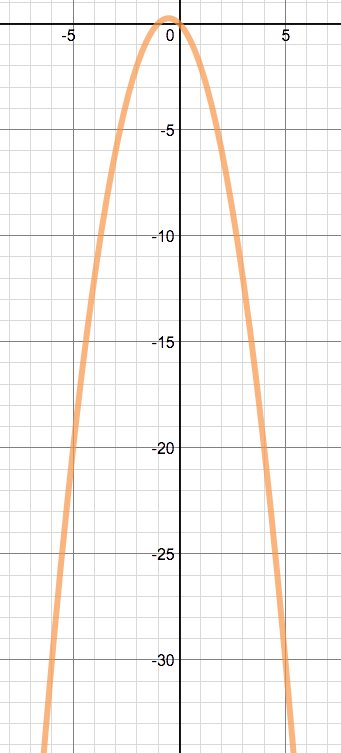
The question now, is how can we find the roots of this equation? One way is to look a the horizontal line that goes through the c-axis. If we plug in y=c, we can look at different values that cross the parabola as well as the roots of the equation.

Here the horizontal line is located at c=-10.
Try manipulate the graph and exploring this situation on Desmos!
From the graph and the varying c, we can see that when c is greater than the vertex of the parabola, (-0.5, 0.25), it follows that the line does not cross the parabola at all.
When c=0.25, the line cross the parabola at only one point. This point being the vertex of the parabola (-0.5, 0.25).
When c less than 0.25, it follows that the line will cross the parabola at two points. There will be one point of intersection on the left of the line x=-0.5 and there will be one point of intersection on the right of the same line.
Now, let's think about what is going on with the points of intersection between the parabola and the horizontal line.
For example, let's take c =-10 which is graphed above. This gives the equation:
![]()
This is a quadratic equation and the quadratic equation can be used to find the roots, points of intersection between the horizontal line and the parabola.
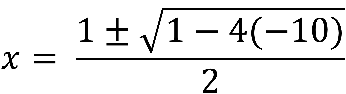
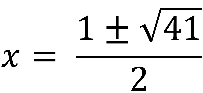
These two points determine where the points are located on the graph.